نظریه گن چیست و چطور می‌توان از آن در تحلیل استفاده کرد؟

از دیرباز معامله‌گران روش‌های متعددی را به عنوان سبک معاملاتی خود انتخاب کرده‌اند که برخی بر پایه‌ی روابط علمی بنا شده‌اند، مثل نظریه امواج الیوت، و برخی دیگر بر اساس تجربه و مشاهده. روش معامله‌ و نظریه گن اگرچه از نظر علمی قابل توجیه نیست، اما یکی از روش‌های معاملاتی بسیار محبوب و مورد استقبال عموم است.

ویلیام گن

ویلیام دلبرت گن در سال ۱۸۷۸ در ایالت تگزاس آمریکا دیده به جهان گشود. او بین سال‌های ۱۹۰۰ تا ۱۹۵۶ به عنوان چنان معامله‌گر بی‌همتایی در بازار سرمایه شناخته شد که القابی همچون معلم وال‌استریت، استاد پیش‌بینی‌های اقتصادی و … را به خود اختصاص داد. نظریه گن یکی از معروف‌ترین نظریه‌های این معامله‌گر شهیر است. او در یک بازه‌ی زمانی بیست و پنج روزه، بازدهی هزار درصدی به‌دست آورد. همچنین میانگین بازده‌های سرمایه‌گذاری‌های وی بین هشتاد تا نود درصد بوده است. موارد خطای او مربوط به نقص روش معاملاتی نبوده، بلکه این موارد مربوط به محاسبات و طراحی خود معامله بوده است. گن در خانواده‌ای مذهبی پرورش یافت و گفته می‌شود بخش‌هایی از کتاب مقدس سرلوحه‌ی کار او بوده است، مانند این عبارت: «هرچیز پیش از این بوده، پس از این هم خواهد بود و هر آنچه پیش از این انجام شده، پس از این هم انجام خواهد شد و هیچ‌چیز زیر این خورشید جدید نیست». گن عقیده داشت نظمی جهانی وجود دارد، از این رو می‌توان تغییرات جهان، از جمله رفتار افراد را با استفاده از روابط ریاضی تجزیه و تحلیل کرده، با کشف روند این روابط، برخی از تغییرات را پیش‌بینی کرد.

ادعاهای ضد و نقیضی درباره‌ی انتقال تجربیات گن وجود دارد؛ مثلاً عده‌ای بر این باورند که وی تجربیات خود را به‌طور کامل به دیگران منتقل نکرده است، زیرا بازدهی کار پیروان او به‌مراتب کمتر از خود گن بوده است. از طرفی، عده‌ای با تکیه بر این سخن گن که می‌گوید «درآمد من بسیار بیشتر از نیازم بوده و تنها انگیزه‌ی من انتقال دانش به دیگران است»، بر این باورند که وی همه‌ی دانش خود را به دیگران منتقل کرده است.

مربع نُه تایی معروف‌ترین نظریه گن

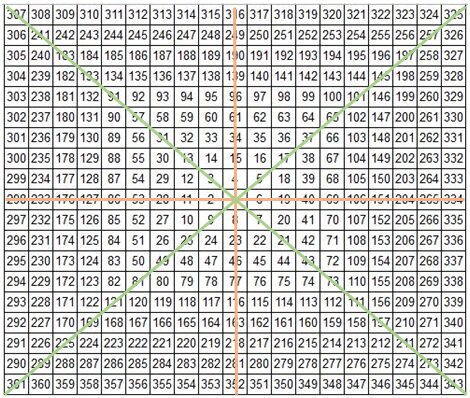
از معروف‌ترین نظریه‌های او می‌توان به مربع نه تایی و زوایای گن اشاره کرد. در دهه‌ی ۱۹۲۰ گن مربع نه تایی خود را معرفی کرد که به آن مربع جادویی یا حسابگر زمان– قیمت نیز می‌گفتند. این مربع از دو بخش تشکیل شده است که شامل یک مربع ۳۶۱ خانه‌ای و یک دایره‌ی محیطی مدرج و یا همان دایره‌ی مثلثاتی می‌شود. به هر خانه‌ی مربع یک سلول می‌گویند که به نام عدد داخل خودش نام‌گذاری شده و شناخته می‌شود. سلول‌ها از شماره‌ی ۱ که در مرکز مربع است، آغاز شده و از سمت چپ در جهت حرکت عقربه‌های ساعت ادامه پیدا می‌کنند تا به عدد ۹ می‌رسند. آنگاه مجدداً از سمت چپ آنریال چرخش بعدی آغاز می‌شود. به هر چرخش ۳۶۰ درجه‌ای این سلول‌ها یک دور یا مربع کامل نیز می‌گویند. هر دور را با بزرگ‌ترین سلول آن نام‌گذاری می‌کنند که درواقع همان آخرین سلول چرخش است. مثلاً دوری که با سلول ۴۹ به پایان می‌رسد را چرخش یا دور ۴۹ می‌نامند.

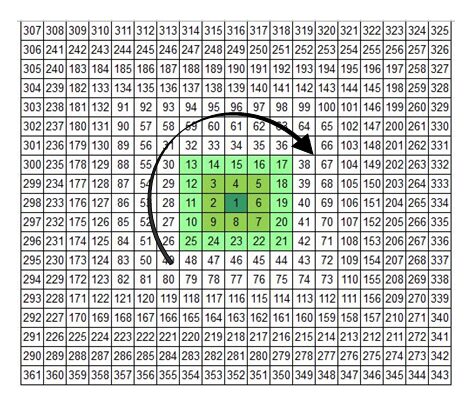
ازجمله ویژگی‌های جالب این مربع، وجود دو ردیف از مجذورات اعداد فرد و زوج متوالی است. مربع گن یک مربع مشبک است که خود آن نیز از ۳۶۱ مربع دیگر تشکیل شده و عدد ۱ مرکز آن و عدد ۳۶۱ در ضلع جنوب غرب آن واقع شده است و به شکل ساعت‌گرد در چرخش‌های متوالی از مرکز مربع به سمت اطراف افزایش می‌یابد. همچنین این مربع توسط دایره‌ای مندرج مهار شده که از ۰ تا ۳۶۰ شماره‌گذاری شده و درواقع معرف درجه است و به‌صورت پادساعت‌گرد (مخالف جهت سلول‌های مربع) افزایش می‌یابد. این مربع به همراه دایره‌ی مندرج اطراف آن، پایه و اساس تمام تحلیل و پیش‌بینی‌هایی است که با تبعیت از برخی قواعد و با استفاده از اجزاء داخل آن انجام می‌شود.  

نقاط میان راهی

نقاط میان راهی در نظریه گن به نقاط بین یک مجذور و مجذور فرد بعد از آن اطلاق می‌شود؛ مثلاً نقطه‌ی میان راهی بین دو عدد ۴۹ و ۶۴، عدد ۵/۵۶ است که در ناحیه‌ی شمال غربی مربع واقع است. همچنین دسته‌ای از این نقاط در ناحیه‌ی جنوب شرقی مربع قرار دارند؛ مانند نقطه‌ی میانی ۶۴ و ۸۱ که عدد ۵/۷۲ بوده و در ناحیه‌ی جنوب شرقی مربع واقع شده است.

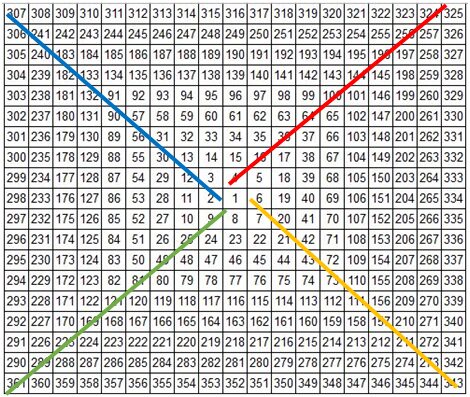
از اتصال فرضی نقاط میان راهی‌که در ناحیه‌ی شمال غرب قرار دارند به یکدیگر و همچنین نقاط میان راهی جنوب شرقی، مکان هندسی این نقاط به دست می‌آید.  

چارک‌ها

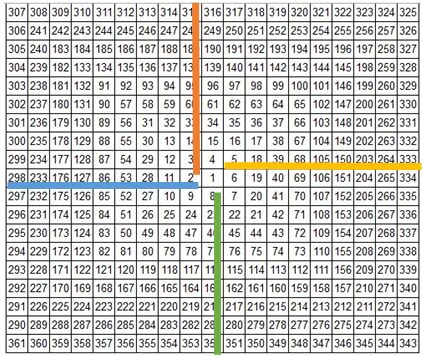
حال اگر حدفاصل بین مجذور کامل زوج و مجذور کامل فرد را به چهار قسمت مساوی تقسیم کنیم، به هر بخش یک چارک گفته می‌شود. نقطه‌ی انتهایی بازه‌ی اول را چارک اول، نقطه‌ی دوم که همان نقطه‌ی میان راهی نیز هست را چارک دوم و نقطه‌ی سوم را چارک سوم گویند. یکی از نکات حائز اهمیت محاسبه چارک‌ها در نظریه گن این است که عموماً چارک‌های اول و سوم عدد صحیح نیستند.  

تقاطع اصلی و تقاطع قطری

دو رکن ساده، ولی اساسی در نظریه گن تقاطع اصلی و قطری هستند. تقاطع قطری از تجمیع مکان هندسی تقریبی مجذورهای کامل فرد و زوج به همراه نقاط میان راهی پدید می‌آید و در واقع شکل نهایی آن به صورت یک ضربدر است. تقاطع اصلی مکان هندسی تقریبی چارک‌های اول و سوم را نشان می‌دهد که مانند یک علامت به‌علاوه (+) است.

محاسبه‌ی تعداد سلول‌های هر چرخش

از ویژگی‌های جالب این مربع، افزایش هشت سلول در هر چرخش نسبت به چرخش قبلی است. دو روش وجود دارند که اگر ما بخواهیم بدون شمارش سلول‌هایی که در یک چرخش و محیط آن مربع وجود دارند، تعداد آن‌ها را محاسبه کنیم در روش اول، ریشه‌ی عددی که چرخش با آن به پایان می‌رسد و آن دور به نام آن نام‌گذاری شده است را به دست می‌آوریم و آن را به دو تقسیم می‌کنیم. سپس اعشار آن را از عدد کسر می‌کنیم تا به یک عدد صحیح برسیم. آنگاه آن عدد را در هشت ضرب می‌کنیم. عدد حاصل‌شده، تعداد سلول‌های محیطی یک چرخش را نشان می‌دهد. در روش دوم، ریشه‌ی خانه‌ی آخر را محاسبه کرده، در چهار ضرب کرده، سپس عدد چهار را از آن کسر می‌کنیم.  

دایره‌ی مربع گن

پیرامون مربع گن، دایره‌ای قرار دارد که از ۱ تا ۳۶۰ درجه شماره‌گذاری شده و به چهار بخش تقسیم می‌شود. این دایره همان دایره‌ی مثلثاتی معروف است. بخش اول، از نقطه‌ی ابتدایی یا زاویه‌ی صفر شروع می‌شود. نقطه‌ی شروع معرف اعتدال بهاری، ۹۰ درجه انقلاب تابستانی، ۱۸۰ اعتدال پاییزی و ۲۷۰ درجه انقلاب زمستانی است. گن برای نمایش زوایا، همواره خطی از مرکز مربع به زاویه‌ی موردنظر رسم می‌کرد و آن خط را زاویه می‌نامید.  

لایه‌ها در نظریه گن

اکنون وقت آن رسیده است که درباره‌ی ابزار مکملی بگوییم که نقش خط‌کش را در طراحی‌ها و محاسبات نظریه گن دارد و اصطلاحاً به آن لایه گفته می‌شود. برای توضیح سازوکار لایه باید فرض کنیم لایه‌هایی شفاف از جنس شیشه وجود دارند که ما می‌توانیم خطوطی را بر روی آن‌ها رسم کنیم. سپس آن‌ها را بر روی مربع گن قرار داده و حرکتشان می‌دهیم. این لایه‌ها به دو دسته‌ی کلی، یعنی لایه‌های زاویه‌ای و لایه‌های شکلی تقسیم می‌شوند. در لایه‌های زاویه‌ای، خطوطی که بر روی لایه ترسیم شده‌اند، حول مرکز خود به چرخش درمی‌آیند. طبق توافقی، نام خطوط، نام همان زاویه‌ای است که می‌سازند. خطوط لایه‌ی دیگری که استفاده می‌کنیم، با هم زاویه‌ی ۶۰ درجه می‌سازند. لایه‌ی خاص دیگری هم وجود دارد که از چهار خط با زوایای ۰.۱۴۴، ۱۸۰.۲۱۶ تشکیل شده است. اما نوع دوم لایه‌ها، لایه‌های شکلی هستند که اساس آن‌ها اشکال هندسی است؛ اشکالی همچون مربع، مثلث و …. دو روش برای تنظیم تراز لایه‌ها با مربع وجود دارند: در اولین روش می‌توان زاویه‌ی صفر لایه‌ها را با زوایای دایره‌ی مندرج تراز کرد. برای مثال اگر زاویه‌ی صفر روی زاویه‌ی ۶۹ درجه‌ی دایره قرار گیرد، می‌گویند لایه با زاویه‌ی ۶۹ تراز شده است. روش و سبک دیگر، تراز کردن زاویه‌ی صفر لایه با سلول‌های مربع گن است. مثلاً اگر زاویه‌ی صفر از مرکز سلول ۸۵ عبور کند، اصطلاحاً می‌گویند لایه با سلول ۸۵ تراز شده است. در روش تراز کردن لایه با سلول‌ها ممکن است زاویه‌ی صفر دقیقاً از مرکز سلول عبور نکند. در این حالت با یک عدد اعشاری تراز خواهد شد.